고정 헤더 영역
상세 컨텐츠
본문
I. 상관분석
1. 개념
(1) 두 변수 간의 선형적 관계가 존재하는지 알아보는 분석방법
(2) 상관계수 활용: 관련성 정도의 측도
(3) 이론적 타당성(독립성) 확인. 독립변수 대상 변수들은 서로 간에 독립적이어야 함.
(4) 독립변수 대상 변수들은 다중공산성이 발생할 수 있는데 이를 확인 가능
(5) 변수 간에 상관관계가 있다는 것은 반드시 그 변수들 사이에 인과관계가 있다는 말은 아님
(6) 인과관계는 회귀분석으로 확인
2. 가설
(1) 귀무가설: 상관계수 = 0 => 두 변수는 아무 상관관계가 없다.
(2) 대립가설: 상관계수 ≠ 0 => 두 변수 간에 유의한 상관관계가 있다
3. 공분산
(1) 두 확률변수 X, Y가 같이 변하는 정도의 측도
(2)
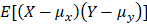
(3)
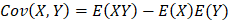
(4)

(5) 두 확률변수 X, Y가 서로 독립이면 Cov(X, Y) = 0 이다
(6) 값의 범위가 정해져 있지 않아 어떤 값을 기준으로 정하기가 모호
(7) 함수
1) numpy모듈: numpy.cov(X, Y) – ndarray로 반환
2) pandas모듈: data.cov() - DataFrame으로 반환(모든 컬럼의 관계를 알 수 있다)
4. 종류
(1) 피어슨 상관분석(선형적 상관관계)
1) 두변수가 모두 정규분포를 따른다는 가정
2) 피어슨 상관계수
① 두 변수 X 와 Y 간의 선형 상관 관계를 계량화한 수치
② 등간 척도나 비례척도의 데이터에서 두 변수의 공분산을 표준 편차의 곱으로 나눈 값

③ 상관계수의 범위: -1 ≤ r ≤ 1
④ r = -1: 음의 상관관계(역상관)
⑤ r = 0
i. X, Y는 독립적
ii. 상관이 없다는 것이 아니라 선형의 상관관계가 아니라는 것
⑥ r = 1: 양의 상관관계(정상관)
⑦ 상관계수의 해석
|
상관계수의 범위 |
상관관계의 언어적 표현 |
|
0.00 ~ 0.20 |
상관이 거의 없다 |
|
0.20 ~ 0.40 |
상관이 낮다 |
|
0.40 ~ 0.60 |
상관이 있다 |
|
0.60 ~ 0.80 |
상관이 높다 |
|
0.80 ~ 1.00 |
상관이 매우 높다 |
⑧ 산점도 그래프

3) 함수
① numpy모듈: numpy. corrcoef(X, Y) – ndarray로 반환
② pandas모듈: data.corr(method='pearson'/ 'spearman'/ kendall') – DataFrame로 반환
i. pearson 상관계수: df.corr(method='pearson')
a. 변수가 등간, 비율, 정규성
b. 디폴트 값
ii. 서열척도, 정규성 X
a. spearman 상관계수: df.corr(method='spearman')
b. kendall 상관계수: df.corr(method='kendall')
4) 상관관계 시각화 종류
import matplotlib.pyplot as plt
m = [-3, -2, -1, 0, 1, 2, 3]
n = [9, 4, 1, 0, 1, 4, 9]
plt.plot(m, n, '+')
plt.show()
import pandas as pd
df.plot(kind='scatter', x='만족도', y='적절성')
plt.show()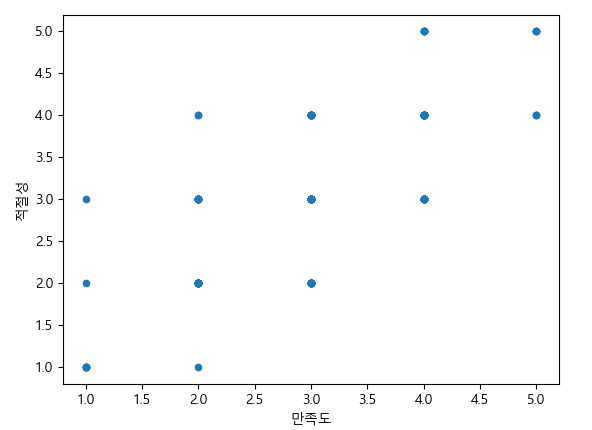
from pandas.plotting import scatter_matrix
attr = ['친밀도', '적절성', '만족도']
scatter_matrix(df[attr], figsize=(10, 6))
plt.show()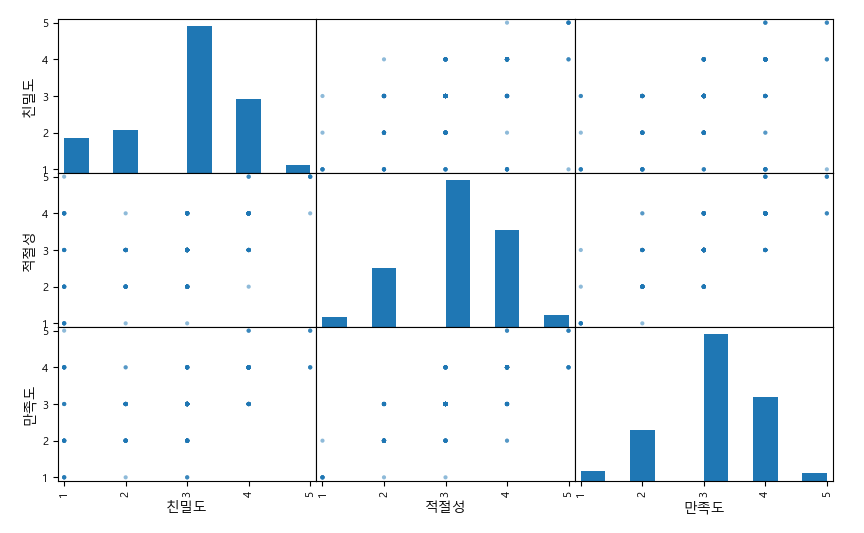
import seaborn as sns
# heatmap: 밀도를 색으로 표현, 색이 진할수록 약한 상관관계
sns.heatmap(df.corr())
plt.show()
# heatmap에 텍스트 표시 추가사항 적용해 보기
corr = df.corr()
# Generate a mask for the upper triangle
mask = np.zeros_like(corr, dtype=np.bool) # 상관계수값 표시
mask[np.triu_indices_from(mask)] = True
# Draw the heatmap with the mask and correct aspect ratio
vmax = np.abs(corr.values[~mask]).max()
fig, ax = plt.subplots() # Set up the matplotlib figure
sns.heatmap(corr, mask=mask, vmin=-vmax, vmax=vmax, square=True, linecolor="lightgray", linewidths=1, ax=ax)
for i in range(len(corr)):
ax.text(i + 0.5, len(corr) - (i + 0.5), corr.columns[i], ha="center", va="center", rotation=45)
for j in range(i + 1, len(corr)):
s = "{:.3f}".format(corr.values[i, j])
ax.text(j + 0.5, len(corr) - (i + 0.5), s, ha="center", va="center")
ax.axis("off")
plt.show()
import matplotlib.pyplot as plt
fig = plt.figure()
fig.suptitle(tourPoint + '상관관계분석')
plt.subplot(1,3,1)
plt.xlabel('중국인 수')
plt.ylabel('외국인 입장객 수')
lamb1 = lambda p:merge_table['china'].corr(merge_table['ForNum'])
r1 = lamb1(merge_table)
plt.title('r={:.3f}'.format(r1))
plt.scatter(merge_table['china'], merge_table['ForNum'], s=6, c='black')
plt.subplot(1,3,2)
plt.xlabel('일본인 수')
plt.ylabel('외국인 입장객 수')
lamb2 = lambda p:merge_table['japan'].corr(merge_table['ForNum'])
r2 = lamb2(merge_table)
plt.title('r={:.3f}'.format(r2))
plt.scatter(merge_table['japan'], merge_table['ForNum'], s=6, c='red')
plt.subplot(1,3,3)
plt.xlabel('미국인 수')
plt.ylabel('외국인 입장객 수')
lamb3 = lambda p:merge_table['usa'].corr(merge_table['ForNum'])
r3 = lamb3(merge_table)
plt.title('r={:.3f}'.format(r3))
plt.scatter(merge_table['usa'], merge_table['ForNum'], s=6, c='blue')
plt.show()
(2) 스피어만 상관분석(비선형적 상관관계)
1) 측정된 두 변수들이 서열 척도일 때 사용하는 상관계수
2) 비모수적 방법으로 관측 값의 순위에 대하여 상관계수를 계산하는 방법
'데이터분석 by파이썬' 카테고리의 다른 글
| 회귀분석 - 2. 선형회귀분석 (0) | 2021.06.01 |
|---|---|
| 회귀분석 - 1. 개요 (0) | 2021.03.22 |
| 분산분석(ANOVA) (0) | 2021.03.10 |
| t – test (0) | 2021.03.09 |
| 교차분석(카이제곱분석) (0) | 2021.03.07 |




