고정 헤더 영역
상세 컨텐츠
본문
(1) 독립변수와 종속변수가 1개씩일 때 둘 사이의 인과관계 분석
(2) 독립변수로 종속변수의 움직임을 예측하고 설명하는 작업
(3) 기존데이터로 잘 그려진 직선으로 아직 답이 나오지 않은 데이터의 답을 예측
(4) 최소제곱법을 활용하여 실제 데이터와 오차가 가장 작아지는 직선의 방정식 찾음

(5) 최소제곱법(Least Squared Method, LSM)
1) 직선을 잘 그리기 위해서 사용하는 도구
2) 실제 관측치와 추세선에 의해 예측된 점 사이의 거리
3) 주어진 독립변수가 한 개일 때 사용 가능
4) 오차를 제곱해서 더한 값(SSE)을 최소화하는 것
5) 자료들 사이에서 패턴을 도출
6) 직선의 오차를 평가하는 오차평가 알고리즘, 비용함수. only 평가
7) 여러 개의 입력 값(x)을 처리할 때 임의의 직선을 그린 후 직선이 얼마나 잘 그려졌는지 평가하여 조금씩 수정해서 최적의 직선을 도출해야 한다
8) 회귀선의 기울기와 y절편 구하기


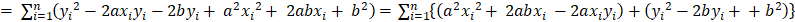
a값과 b값을 구하기 위해서 a에 대한 편미분, b에 대한 편미분 진행
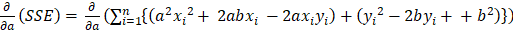

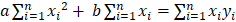



㉠와 ㉡를 행렬식으로 만들면




※ 비용함수(Cost function) = 손실함수(Loss function), 목적함수(Objective function)
n 기울기(가중치), y절편(bias)와 오차의 관계를 함수로 나타낸 것 ex) MSE
n 선형회귀분석에서는 이차함수의 그래프로 나타낸다
n 로지스틱 회귀분석에서는 로그함수를 이용하여 나타낸다
n 공통점은 이 손실함수의 최소값을 구하기 위해서는 편미분 사용
n 머신러닝 모델의 평가 지표를 정의
n 모델과 훈련 샘플의 적합 정도 나타냄
n 서로 다른 손실함수에 따라 최적화 난이도가 다르고, 최종적으로 얻는 모델 파라미터도 다름
(6) 평균제곱오차(Mean Square Error, MSE), 제곱오차함수(Squared Error Function)

① 예측이 실제 결과에 얼마나 가까운지를 측정
② 점수가 낮을수록 좋음
(7) 경사하강법
1) x입력 값이 많아지면 편차의 수(n)가 커지므로 최소제곱법을 적용하기 어려움
2) SSE에서 기울기 또는 y절편과 오차의 관계는 이차함수 모양의 아래로 볼록 그래프로 그려짐
3) 이때 이차함수의 최소값을 만드는 기울기를 찾는데 즉, 이차함수 미분 값이 0이 되는 지점을 구하면 된다.
4) 경사하강법(gradient descent): 이 그래프에서 오차를 비교하여 미분 값이 가장 작은 방향으로 이동시키는 방법
5) 신경망의 노드가 많아지면 독립변수가 많아지는 것과 유사한 형태이므로 보통 딥러닝에서 사용
6) 경사하강법 과정


① a1에서 미분 구한다
② 구해진 기울기의 반대방향(기울기가 +면 음의 방향, -면 양의 방향)으로 얼마간 이동시킨 a2에서 미분 구하기
③ 미분 값이 0이 될 때까지 반복
④ y절편과 오차와의 관계도 위와 같은 성질을 가지고 있다. => 최적의 y절편을 구할 때도 경사하강법 사용
⑤ 기울기가 필요할 때는 기울기로 평균제곱오차를 편미분하고, y절편이 필요할 때는 y절편으로 평균제곱오차를 편미분 한다.

7) 단점: 최적의 가중치를 찾기 위해 업데이트할 때마다 전체 데이터를 미분해야 하므로 계산량이 많음
(8) 경사하강법 보완한 고급 경사 하강법
1) 확률적 경사 하강법(Stochastic Gradient Descent, SGD)
① 계산량이 많은 일반 경사하강법을 보완하여 속도를 높이기 위해 등장
② 업데이트할 때 전체데이터를 사용하지 않고 랜덤하게 추출한 일부 데이터를 사용하여 더 빠르고 자주 업데이트 가능
③ 랜덤한 일부 데이터를 사용하므로 중간 결과의 진폭이 크고 불안정해 보이지만 빠르면서 최적 해에 근사한 값을 찾아낸다는 장점을 가짐

2) 개발된 순서 – 먼저 나온 방법의 단점을 보완하여 다음 방법이 나온 것이므로 마지막의 아담이 가장 좋은 성과를 보임. 그래서 가장 많이 사용되는 경사하강법
| 고급 경사 하강법 | 개요 | 효과 | keras 사용법 |
| 확률적 경사 하강법(SGD) | 랜덤하게 추출한 일부 데이터를 사용해 더 빨리, 자주 업데이트를 하게 하는 것 | 속도 개선 | keras.optimizers.SGD(lr = 0.1) 케라스 최적화 함수를 이용합니다. |
| 모멘텀(Momentum) | 관성의 방향을 고려해 진동과 폭을 줄이는 효과 | 정확도 개선 | keras.optimizers.SGD(lr = 0.1, momentum = 0.9) 모멘텀 계수를 추가합니다. |
| 네스테로프 모멘텀(NAG) | 모멘텀이 이동시킬 방향으로 미리 이동해서 gradient계산. 불필요한 이동을 줄이는 효과 | 정확도 개선 | keras.optimizers.SGD(lr = 0.1, momentum = 0.9, nesterov = True) 네스테로프 옵션을 추가합니다. |
| 아다그라드(Adagrad) | 변수의 업데이트가 잦으면 학습률을 적게 하여 이동 보폭을 조절하는 방법 | 보폭 크기 개선 | keras.optimizers.Adagrad(lr = 0.01, epsilon = 1e - 6) 아다그라드 함수를 사용합니다. ※ 참고: 여기서 epsilon, rho, decay 같은 파라미터는 바꾸지 않고 그대로 사용하기를 권장하고 있습니다. 따라서 lr, 즉 learning rate(학습률) 값만 적절히 조절하면 됩니다. |
| 알엠에스프롭(RMSProp) | 아다그라드의 보폭 민감도를 보완한 방법 | 보폭 크기 개선 | keras.optimizers.RMSprop(lr = 0.001,rho = 0.9, epsilon = 1e - 08, decay = 0.0) 알엠에스프롭 함수를 사용합니다. |
| 아담(Adam) | 모멘텀과 알엠에스프롭 방법을 합친 방법 | 정확도와 보폭 크기 개선 | keras.optimizers.Adam(lr = 0.001, beta_1 = 0.9, beta_2 = 0.999, epsilon = 1e - 08, decay = 0.0) 아담 함수를 사용합니다. |
(9) hyper parameter(learning rate, epoch, batch-size)를 결정하는 일은 데이터 분석가가 하는 일
1) epoch: 입력 값에 대해 몇 번이나 반복해서 실험했는지 나타냄
2) learning rate
① 기울기의 부호를 바꿔 이동시킬 때 이동거리를 정해주는 것
② 적절한 거리를 찾지 못하면 기울기 a가 수렴하지 못하고 발산함

③ 학습률, 가중치와 bias 값의 감소 또는 증가 비율을 나타냄
④ learning rate이 너무 적으면 처리 속도가 느리고, 너무 크면 부정확
3) 배치(batch)
① 훈련 데이터의 샘플은 여러 개로 묶여서 학습되는데 이 샘플의 묶음
② 1 epoch에 이용되는 훈련 데이터는 여러 개의 batch로 분할됨
☞ 결론: 선형회귀란 임의의 직선을 그어 이에 대한 평균 제곱오차를 구하고, 이 값을 가장 적게 만들어 주는 직선의 기울기와 y절편을 찾아가는 작업
[참조] From the bottom :: 에포크와 배치(Epoch and Batch) (tistory.com)
(1) 독립변수가 2개 이상이고 종속변수가 하나일 때, 사용 가능한 회귀분석으로 독립변수와 종속변수의 관계가 선형으로 표현된다.
(2) 독립변수가 여러 개 이므로 회귀계수(기울기)도 여러 개이다.
(3) 다중공선성
1) 회귀분석에서 독립변수 간에 강한 상관관계가 나타나는 문제
2) 다중공선성이 존재하면 회귀분석의 기본 가정인 독립성에 위배됨
3) 다중공선성이 존재하면 각각의 독립변수가 종속변수에 어느 정도의 영향을 미치는지 정확하게 판단 불가
4) 결정계수 값은 큰데 독립변수의 p-value도 커서 개별 인자가 유의하지 않은 경우 의심
5) 분산팽창요인(Variance Inflation Factor, VIF): 다른 변수의 선형결합으로 x_i를 설명할 수 있는 정도
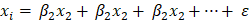
이 회귀모델의 결정계수로 VIF_i 계산

6) VIF > 10(결정계수 > 0.9): 다중 공선성이 있다고 판단
(4) 다중 공선성 해결
1) 문제가 발생하는 변수 제거
① VIF가 높더라도 통계적으로 유의미한 변수(p-value가 유의수준 보다 낮은 변수)라면 제거하지 않는 것이 적절
② 다른 변수들 중에 VIF가 높고, 유의미하지 않은 변수가 있다면 그 변수들을 제거해 본 뒤 VIF를 다시 계산
2) 주성분 분석(PCA)을 통해 변수의 차원을 축소: 변수를 삭제하여 차원을 줄이는 것이 아니라 원래 데이터가 가진 내재적 속성을 보존하면서 데이터를 축소
3) 선형판별분석(LDA)로 차원 축소
4) t-분포 확률적 임베딩(t-SNE)로 차원축소
5) 특잇값 분해(SVD)로 차원 축소
[참고] Regression(02) - 다중선형회귀 및 다중공선성 | DataLatte's IT Blog (heung-bae-lee.github.io)
'데이터분석 by파이썬' 카테고리의 다른 글
| 회귀분석 - 4. 회귀분석 결과 해석 (0) | 2021.06.01 |
|---|---|
| 회귀분석 - 3. 유의성 검증, 결정계수 (0) | 2021.06.01 |
| 회귀분석 - 1. 개요 (0) | 2021.03.22 |
| 상관분석 (0) | 2021.03.12 |
| 분산분석(ANOVA) (0) | 2021.03.10 |




