고정 헤더 영역
상세 컨텐츠
본문
(1) 개념
1) 하나 이상의 독립변수들이 종속변수에 얼마나 영향을 미치는지 추정하는 통계기법
2) 독립변수와 종속변수 간에 인과관계가 있다
① 독립변수가 원인이 되어 종속변수에 영향을 미친다
② 변수들이 일정한 경향을 띤다
③ 산점도 그래프가 일정한 추세선(직선형태, 포물선형태)을 나타낸다
3) 독립변수 = 원인변수 = 설명변수
4) 종속변수 = 결과변수 = 반응변수
5) 독립변수: 연속형, 종속변수: 연속형
6) 종속변수가 범주형 일 경우 로지스틱 회귀분석 사용
7) 회귀(Regression)
① 회귀의 원래 의미는 옛날 상태로 돌아가는 것을 의미
② 영국의 유전학자 프랜시스 골턴은 부모의 키와 아이들의 키 사이의 연관 관계를 연구하면서 부모와 자녀의 키사이에는 선형적인 관계가 있고 키가 커지거나 작아지는 것보다는 전체 키 평균으로 돌아가려는 경향이 있다는 가설을 세웠으며 이를 분석하는 방법을 "회귀분석"이라고 하였다. 이러한 경험적 연구 이후, 칼 피어슨은 아버지와 아들의 키를 조사한 결과를 바탕으로 함수 관계를 도출하여 회귀분석 이론을 수학적으로 정립하였다.
(2) 회귀 분석의 표준 가정(전제조건)
1) 선형성
① 독립변수와 종속변수가 선형적이어야 한다
② 예외적으로 2차함수 회귀선을 갖는 다항회귀분석의 경우에는 선형성을 갖지 않아도 된다.
③ 산점도를 통해 분석하기 전에 변수사이의 관계를 짐작할 수 있어 회귀분석 하기 전 상관분석은 거의 필수적이다.
2) 독립성
① 단순회귀분석에서 잔차와 독립변수의 값이 서로 독립적
② 다중회귀분석에서는 독립변수들이 서로 독립적
3) 다중공선성
① 다중회귀분석에서 독립변수들 간에 독립적이지 않고 상관성이 존재하는 경우
② 이를 제거하고 회귀분석 시행해야 한다
4) 등분산성
① 분산이 같다 = 잔차들이 고르게 분포되어 있다
② 잔차의 중심에서 분산이 같아야 한다
③ 등분산성을 만족하지 못하면 회귀선은 덩어리 모양을 하게 된다.
④ 오차(혹은 잔차)의 분산이 입력변수와 무관하게 일정
⑤ 오차와 입력변수 간에 아무런 관련성이 없게 무작위적으로 고루 분포되어야 함

⑥ ∩ 모양의 그래프는 X값이 커짐에 따라 잔차가 커지거나 작아지거나 하기 때문에 오차와 입력변수 간에 아무런 관련성이 없다고 보기 힘듦
⑦ 우상향 그래프에서 X값이 커짐에 따라 잔차가 커지는 모습을 보여 오차와 입력변수 간에 아무런 관련성이 없다고 보기 힘듦
5) 정규성
① 잔차항이 정규분포 형태를 띠는 것
② 오차항의 평균(기대값)은 0이다
③ Q-Q plot에서 잔차가 오른쪽으로 상승하는 형태를 띠면 정규성을 만족한다고 판단
※ 오차와 잔차
n 오차: 모집단의 데이터를 활용하여 회귀 식을 구한 경우 예측 값과 실제 값의 차이
n 잔차: 표본집단에 의해 추정된 회귀식의 예측 값과 실제 값의 차이
※ 잔차도: 예측 값과 실제 값의 차이를 나타낸 산점도
(3) 전제조건 확인 함수
1) 잔차항: 실제 값 – predict(), polyval()
2) 선형성: 패턴확인 - 시각화
① 예측값과 잔차가 비슷하게 유지되어야 함
② 파선을 기준으로 근사하게 잔차선이 그려져야 선형성을 이룬다 라고 말 할 수 있다.
sns.regplot(fitted, residual, lowess=True, line_kws={'color':'red'}) # 잔차의 추세선
plt.plot([fitted.min(), fitted.max()], [0, 0], '--', color='gray')
# x축 범위, y축 범위, 선 종류
plt.show()
③ 종속변수가 비선형을 이루는 경우

i. 일반 선형회귀분석을 사용하면 예측한 y값이 실제 값과 차이가 많이 나게 된다.
ii. 따라서 다항 회귀를 사용한다.
iii. 다항회귀: 데이터들 간의 형태가 비선형일 때 데이터에 각 특성의 제곱을 추가해주어서 특성이 추가된 비선형 데이터를 선형 회귀 모델로 훈련시키는 방법
iv. from sklearn.preprocessing import PolynomialFeatures
a. poly = PolynomialFeatures(degree = 2 , include_bias = True)
ü 현재 데이터를 다항식 형태로 변경: 각 독립변수의 회귀계수(기울기) 제곱 혹은 그 이상을 추가
ex) degree=2일 때 [a, b]에 PolynomialFeatures를 적용하면 다음과 같이 반환

ü degree 옵션으로 차수를 조절한다.
ü include_bias 옵션은 True로 할 경우 0승(1)도 함께 만든다.
b. poly.fit_transform(X)
ü 모델생성
ü 매개변수 X를 poly의 다항식에 맞게 형태 변환시킨 후 모델 생성
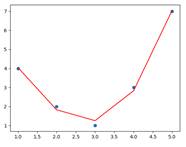
#비선형인 경우 다항식의 특징을 추가해서 작업
from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(degree=3, include_bias=False) # degree 열 개수, include_bias 편향
x2 = poly.fit_transform(x) # 특징행렬을 만듦
print(x2)
print()
model2 = LinearRegression().fit(x2, y)
y_pred2 = model2.predict(x2)
print(y_pred2)
plt.scatter(x, y)
plt.plot(x, y_pred2, c='red')
plt.show()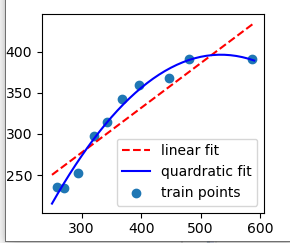
3) 정규성: 잔차가 정규분포를 따르는지 확인
① 패턴확인 – 시각화
i. scipy.stats.zscore(x): 표본 평균 및 표준 편차를 기준으로 표본에 있는 각 값의 z 점수를 계산
ii. scipy.stats.probplot(x, fit=False, plot=None)
a. probability plot에 대한 분위수를 계산하고 선택적으로 플롯을 표시
b. 지정된 이론적 분포 (기본적으로 정규 분포)의 분위수에 대한 표본 데이터의 probability plot를 생성
c. probplot선택적으로 데이터에 가장 적합한 선을 계산하고 Matplotlib 또는 지정된 플롯 함수를 사용하여 결과를 플로팅
d. (osm, x) 튜플 형태 반환
ü osm(order statistic medians): 순서 통계량인 중앙값
ü 순서통계량(order statistic): n개 표본의 측정값들을 그 크기 순으로 작은 쪽부터 배열한 것
ü 최소값, 최대값, 중앙값(median), 4분위수(quantile) 등이 대표적인 순서 통계량
ü i번째 순서 통계량은 n개 요소 가운데 i번째로 작은 값
ü 분위수: 오름차순 혹은 내림차순으로 정렬된 어떤 데이터를 특정 개수로 나눌 때 기준이 되는 수
ü 예를 들어 데이터를 두 개로 나눌 때 둘로 나누는 기준이 되는 수가 이분위수고 네 개로 나눌 때 넷으로 나누는 기준이 되는 수들이 사분위수다.
ü 일반화해서 q분위수라고 한다.
e. (slope, intercept, r) float의 튜플, 선택 사항
ü r 은 결정 계수의 제곱근
ü fit=False와 plot=None인 경우 튜플은 반환X
sr = scipy.stats.zscore(residual)
(x, y), _ = scipy.stats.probplot(sr)
sns.scatterplot(x, y)
plt.plot([-3, 3], [-3, 3], '--', color='gray')
plt.show()
② shapiro로의 p-value로 확인
4) 독립성: 모델.summary()의 Durbin-Watson로 확인
① 2에 가까우면 자기상관이 없다=서로 독립(잔차끼리 상관관계가 없다)
② 0에 가까우면 양의 상관, 4에 가까우면 음의 상관
5) 등분산성: 패턴확인 - 시각화
① 수평선이 그려져야 등분산성이 성립하게 됨
import seaborn as sns
sns.regplot(fitted, np.sqrt(np.abs(sr)), lowess=True, line_kws={'color':'red'})
plt.show()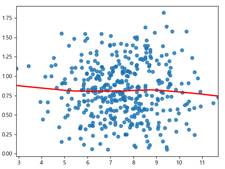
6) 다중공산성: from statsmodels.stats.outliers_influence import variance_inflation_factor
① variance_inflation_factor(data.values, n)
i. data: 범주형 데이터가 없는 DataFrame형태
ii. n: data의 컬럼번호
iii. n번째 컬럼을 종속변수로 나머지는 독립변수로 보았을 때 n번째 컬럼의 VIF 값
from statsmodels.stats.outliers_influence import variance_inflation_factor
print(variance_inflation_factor(data.values, 0))
print(variance_inflation_factor(data.values, 1))
print(variance_inflation_factor(data.values, 2))
print(variance_inflation_factor(data.values, 3))
print(variance_inflation_factor(data.values, 4))
print(variance_inflation_factor(data.values, 5))
print(variance_inflation_factor(data.values, 6))
# DataFrame으로 보기
vifdf = pd.DataFrame()
vifdf['vif_value'] = [variance_inflation_factor(data.values, i) for i in range(data.shape[1])]
vifdf['name'] = data.columns
print(vifdf)7) 이상치 측정
① from statsmodels.stats.outliers_influence import OLSInfluence
② cd, _ = OLSInfluence(모델).cooks_distance: 극단값을 나타내는 지표 반환(cd)
③ 시각화: 원이 클수록 이상치
i. import statsmodels.api as sm
ii. sm.graphics.influence_plot(model, criterion='cooks')
<예제>
from statsmodels.stats.outliers_influence import OLSInfluence
lm_mul = smf.ols(formula='sales ~ tv + radio + newspaper', data = adfdf).fit()
cd, _ = OLSInfluence(lm_mul).cooks_distance
print(cd.sort_values(ascending=False).head())
# 130번째, 5번째, 75번째, 35번째, 178번째가 극단값
import statsmodels.api as sm
sm.graphics.influence_plot(lm_mul, criterion='cooks')
plt.show()
# 원이 큰것들이 극단값
# 극단값은 제거하는게 좋다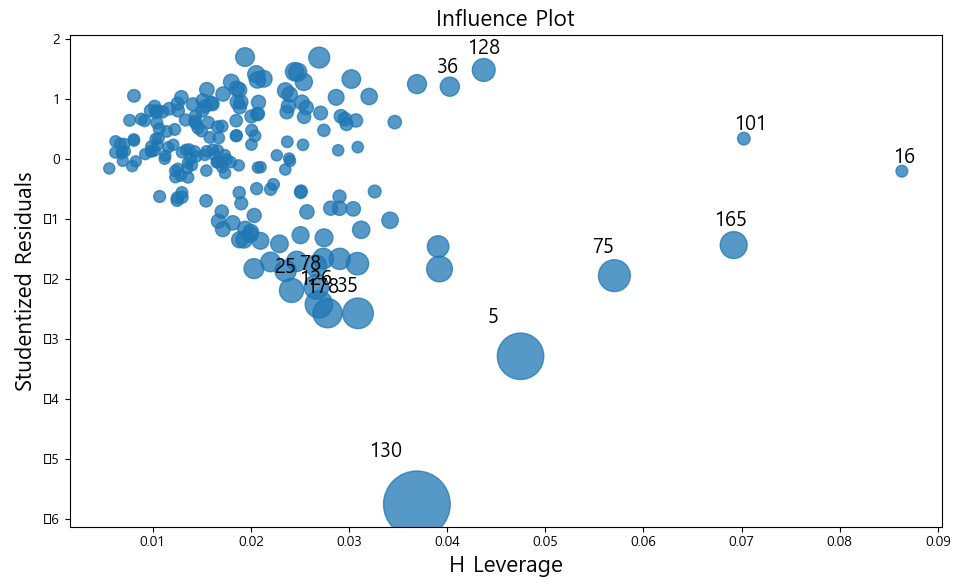
'데이터분석 by파이썬' 카테고리의 다른 글
| 회귀분석 - 3. 유의성 검증, 결정계수 (0) | 2021.06.01 |
|---|---|
| 회귀분석 - 2. 선형회귀분석 (0) | 2021.06.01 |
| 상관분석 (0) | 2021.03.12 |
| 분산분석(ANOVA) (0) | 2021.03.10 |
| t – test (0) | 2021.03.09 |




