고정 헤더 영역
상세 컨텐츠
본문
<import scipy.stats as stats>
< import pandas as pd>
I. 교차분석(카이제곱분석)
1. 데이터나 집단의 분산을 추정하고 검정할 때 사용
2. 검정통계량으로 카이제곱 통계량 사용
3. 독립변수, 종속변수: 범주형(건수, 개수)
4. 일원카이제곱: 변인 단수 => 적합성, 선호도 - 교차분할표 미사용
(1) 범주형 변수가 한 가지로, 관찰도수가 기대도수에 일치하는지 검정한다.
(2) 함수: stats.chisquere(관찰빈도, [기대빈도])
1) 변수가 한 개일 때 사용하는 함수(기대빈도와 관찰빈도의 차이)
2) 관찰빈도와 기대빈도의 전체 수가 같아야 함
import pandas as pd
import scipy.stats as stats
data = [4, 6, 17, 16, 8, 9] # 관찰빈도수 - 귀무가설 기각 데이터
# data = [11, 5, 10, 14, 10, 10] # 관찰빈도수 - 귀무가설 채택 데이터
print(stats.chisquare(data))
# statistic(검정통계량)=14.200000000000001, pvalue=0.014387678176921308
print()
data2 = [10, 10, 10, 10, 10, 10]
print(stats.chisquare(data, data2)) # 기대가설을 안써줘도 된다.
result = stats.chisquare(data)
print('검정통계량(chi^2) = %.5f, p-value = %.5f'%result) # 반비례 관계
# 결론1: p-value 0.01439 < 유의수준 0.05이므로 유의미한 수준에서 (a = 0.05)에서 귀무가설 기각, 연구가설 채택
# 자유도(df) = 6-1 = 5, 임계값: 카이제곱분포표를 참고했을 때 11.07
# 결론2: 검정통계량(chi^2) 14.20000 > 임계값 11.07이므로 귀무가설 기각역에 포함됨. 귀무가설 기각, 연구가설 채택
# 관찰빈도가 기대빈도와 의미있는 차이가 있는지를 검증하기 위해 일원 카이제곱검정을 실시함.
(3) 종류: 적합도/선호도 검정
1) 자연현상이나 각종 실험을 통해 관찰되는 도수들이 귀무가설 하의 분포(범주형 자료의 각 수준별 비율)에 얼마나 일치하는가에 대한 분석
2) 관측값들이 어떤 이론적 분포를 따르고 있는지를 검정으로 한 개의 요인을 대상으로 함.
(4) 자유도(df): 자료의 개수 - 1
5. 이원카이제곱: 변인 복수 => 독립성, 동질성 - 교차분할표 사용
(1) 두 개 이상의 변인(집단 또는 범주)을 대상으로 검정을 수행한다.
(2) 분석대상의 집단 수에 의해서 독립성 검정과 동질성 검정으로 나뉜다.
(3) 독립성(관련성) 검정: 두 변인의 관계가 독립인지를 검정
1) 동일 집단의 두 변인(학력수준과 대학진학 여부)을 대상으로 관련성이 있는가 없는가?
2) 독립성 검정은 두 변수 사이의 연관성을 검정한다.
(4) 동질성 검정
1) 두 집단의 분포가 동일한가? 다른 분포인가?를 검증하는 방법
2) 두 집단 이상에서 각 범주(집단) 간의 비율이 서로 동일한가를 검정
3) 두 개 이상의 범주형 자료가 동일한 분포를 갖는 모집단에서 추출된 것인지 검정하는 방법
(5) 함수
1) 교차표 만들기: pd.crosstab(index=독립변수, columns=종속변수)
2) 변수가 두개 이상 일 때 사용하는 함수: stats.chi2_contingency(data)
① 카이제곱 통계량, p-value, 자유도, 기대도수표 반환
② chi2, p, ddof, expected = stats.chi2_contingency(data)
# 실습) 국가전체와 지역에 대한 인종 간 인원수로 독립성 검정 실습
# 두 집단(국가전체 - national, 특정지역 - la)의 인종 간 인원수의 분포가 관련이 있는가?
# 가설설정
# 귀무가설: 국가전체와 특정지역에 대한 인종 간 인원수의 분포는 관련 없다. 독립
# 대립가설: 국가전체와 특정지역에 대한 인종 간 인원수의 분포는 관련 있다. 종속
national = pd.DataFrame(["white"] * 100000 + ["hispanic"] * 60000 + ["black"] * 50000 + ["asian"] * 15000 + ["other"] * 35000)
la = pd.DataFrame(["white"] * 600 + ["hispanic"] * 300 + ["black"] * 250 + ["asian"] * 75 + ["other"] * 150)
na_table = pd.crosstab(index = national[0], columns='count')
la_table = pd.crosstab(index = la[0], columns='count')
print(la_table)
print()
na_table['count_la'] = la_table['count']
print(na_table)
print()
chi, p, ddof, expected = stats.chi2_contingency(na_table) # R과 동일한 결과를 얻는 함수
print('검정통계량(chi^2) = ',chi) # 18.099524243141698
print('p-value = ',p) # 0.0011800326671747886
print('ddof: ', ddof) # 자유도
print('expected, 기대도수표\n', expected) # 기대도수표
# 결론: p-value 0.0011800326671747886 < 유의수준 0.05 이므로 귀무가설 기각. 대립가설 채택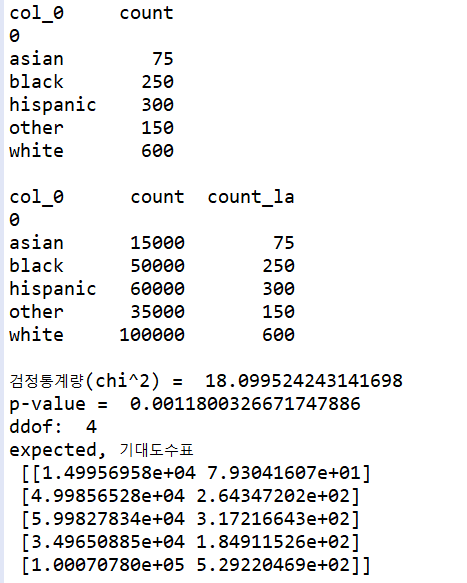
(6) 자유도(df): (행 개수 -1) * (열 개수 -1): 변수가 2개니깐 각각의 자유도 구해서 곱하기
6. 관련용어
(1) 교차표: 2개의 조사 요인에 대한 자료 값을 각각 행과 열로 배열하여 교차되는 항목에 대한 빈도를 나타낸 표
ex)

(2) 관측빈도(observed frequency, ): 실제로 수집된 데이터의 빈도
(3) 기대빈도(expected frequency, )
1) 전체 빈도 n에 대하여 행과 열의 합을 기준으로 보았을 때, 각 교차되는 셀에 기대될 수 있는 기대 값
2)
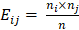
(4) 교차분석에서의 카이제곱 통계량
1) 관측빈도와 기대빈도 사이에 유의한 차이가 있는지를 확인하는 통계량으로 사용
2) 카이제곱 검정은 범주형 변수를 대상으로 연관성을 판단하므로, 범주형 변수의 개수가 k라면 자유도는 k-1로 계산
3)
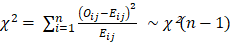
[참고] [기초통계] 연관성 분석, 교차분석(교차표, 적합도검정, 독립성검정) (tistory.com)
'데이터분석 by파이썬' 카테고리의 다른 글
| 분산분석(ANOVA) (0) | 2021.03.10 |
|---|---|
| t – test (0) | 2021.03.09 |
| 통계분석 - 추정과 가설검정 (0) | 2021.03.07 |
| 통계분석 - 통계 개념 (0) | 2021.03.07 |
| 통계분석 - 확률과 확률분포 (0) | 2021.03.07 |




