고정 헤더 영역
상세 컨텐츠
본문
(1) 추정과 가설검정
1) 추정
① 모수의 추정
i. 모수: 모집단의 확률분포 및 특성을 알려주는 모평균과 모분산 같은 값들
ii. 모집단 전체를 대상으로 조사하는 것은 거의 불가능해서 대부분 표본조사를 실시하여 모수를 추정
② 점추정
i. 모수, 특히 모평균을 추정할 때 모평균을 하나의 특정한 값이라고 예측
ii. 모평균을 추정하기 위한 불편추정량은 표본평균이 대표적
iii. 불편(unbiased)추정량
a. 모수를 추정할 때 추정하는 값과 실제 모수 값의 차이의 기댓값이 0으로 어느 한쪽으로 편향되지 않아 모수를 추정하기에 이상적인 값
b. 최소의 분산을 가진 추정량이 가장 좋은 추정량
③ 구간추정
i. 모수가 특정한 구간 안에 존재할 것이라고 예상하는 것
ii. 모수가 특정 구간 안에 포함될 확률인 신뢰도(신뢰수준)가 필요
iii. 신뢰구간 구할 때 모분산이 주어진 경우에는 표준정규분포표의 값을 사용
iv. 모분산이 주어지지 않은 경우 표본분산을 사용할 때는 t분포표의 값으로 계산
2) 가설검정
① 모집단의 특성에 대한 주장 또는 가설을 세우고 표본에서 얻은 정보를 이용해 가설이 옳은지를 판정하는 과정
② 사실 여부에 관계없이 일단 맞다는 것으로 가정을 한 후 그 가정이 참인지 거짓인지 검증하는 과정

③ 귀무가설(null hypothesis)
i. 모집단이 어떠한 특징을 지닐 것으로 여겨지는 가설
ii. 일반적으로 ‘차이가 없다.’, ‘같다’를 사용하여 나타낼 수 있는 가설
iii. 실험, 연구를 통해 기각하고자 하는 어떤 가설
④ 대립가설(alternative hypothesis)
i. 귀무가설이 틀렸다고 판단될 경우 채택되는 가설
ii. 실험, 연구를 통해 증명하고자 하는 새로운 아이디어 혹은 가설
⑤ 제1종 오류와 제2종 오류
i. 제1종 오류: 귀무가설이 사실인데 틀렸다고 결정하는 오류
ii. 제2종 오류: 귀무가설이 사실이 아님에도 귀무가설이 옳다고 결정하는 오류
iii. 제1종 오류와 제2종 오류는 서로 반비례관계라서 한쪽의 오류를 낮추면 나머지 한쪽의 오류는 증가
|
검정결과 |
실제 |
|
|
귀무가설 참 |
귀무가설 거짓 |
|
|
채택 |
참 확률 = 1 – 유의수준 |
거짓(제2종 오류) |
|
기각 |
거짓(제1종 오류) 확률 = 유의수준 |
참 |
iv. 제1종 오류가 더 위험
예를 들어, 한 제약회사의 연구원이 신약(두통약) 아이디어를 제시
개발과 생산 비용은 절약하면서 효과는 5배 이상 좋다는 의견
귀무가설: 기존의 약과 신약의 효과 차이는 없다.
대립가설: 기존의 약과 신약의 효과 차이는 있다. = 신약 효과가 5배이상 좋다
이 연구원이 한 주장이 옳았음에도 계속해서 기존약을 고집한다면 제2종 오류를 범하게 되는 것
기존방식을 고집한다고 해서 두통약 생산 및 매출에 큰 손해는 없음
이 연구원의 주장이 틀렸는데 신약 개발을 할 경우에는 제1종 오류를 범하게 된다.
새로운 신약을 도입하는 데 많은 돈과 시간, 인력 등 투자했는데 기존 두통약과 비교하여 매출에 차이가 없다면 막대한 손실 발생
⑥ 검정방법
i. 양측검정
a. 기각역이 양쪽에 존재
b. 대립가설이 아니다, 크거나 작다라고 할 때 사용

ii. 우측검정
a. 기각역이 우측에만 존재
b. 대립가설이 ~보다 크다라고 할 때 사용
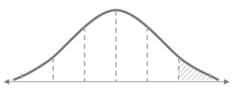
iii. 좌측검정
a. 기각역이 좌측에만 존재
b. 대립가설이 ~보다 작다인 경우에 사용

⑦ 기각역
i. 귀무가설을 기각하게 될 검정통계량 영역
ii. 검정통계량이 기각역 내에 있으면 귀무가설 기각
⑧ 임계값(critical value): 기각역의 경계값
⑨ 유의수준(significance level, α): 귀무가설이 참인데도 이를 잘못 기각하는 오류를 범할 확률의 최대 허용 한계
⑩ 유의확률(significance probability p-value)
i. 귀무가설을 지지하는 정도를 나타낸 확률
ii. p-value가 유의수준α보다 작은 경우에는 귀무가설이 참임을 가정했을 때 이러한 결과가 나올 확률이 매우 적다라고 해석 => 귀무가설 기각, 대립가설 채택
a. p-value < 유의수준α: 귀무가설 기각, 대립가설 채택
b. p-value > 유의수준α: 귀무가설 채택, 대립가설 기각
⑪ 검정 통계량(test statistic): 귀무가설 채택 여부를 판단하기 위하여 표본조사를 실시하였을 때 특정 수식에 의하여 표본 들로부터 얻을 수 있는 값
|
가설검정 |
검정통계량 |
|
z-검정 |
z-통계량 |
|
t-검정 |
t-통계량 |
|
분산분석 |
F-통계량 |
|
카이제곱 검정 |
카이제곱 통계량 |
3) 비모수 검정
① 정규분포를 따르지 않은 경우 자료를 크기순으로 배열하여 순위를 매긴 다음 순위의 합을 통해 차이를 비교하는 순위합 검정 적용할 수 있는데 이런 방법들은 모수의 특성을 사용하지 않는다고하여 비모수검정이라고 한다.
② 숫자로 표현되지 않지만 수량화 할 수 없고 평균을 낼 수도 없는 서열척도의 경우에는 비록 연속형 자료는 아니지만, 순위의 합을 이용하는 비모수적 방법을 적용하는 것 가능
③ 이상치로 인해 평균보다는 중앙값이 더 바람직한 경우, 표본의 크기가 작은 경우, 순위와 같은 서수 데이터인 경우에 사용
|
모수검정(parametric test) |
비모수검정(non parametric test) |
|
모집단이 정규분포라는 가정을 할 수 있는 경우 사용 |
모집단이 정규분포라는 가정을 할 수 없는 경우 사용 |
|
모수분포에 정규화 가정 |
모수의 분포에 가정하지 않음 |
|
등간척도, 비율척도 |
명목척도, 서열척도 |
|
평균 |
중앙값 |
|
피어슨 상관계수 |
스치어만 순위상관계수 |
|
one-sample t-test, two-sample t-test, paired t-test, one way anova |
부호검정, Wilcoxon 부호순위검정, Mann-Whitney검정, Kruskal Wallis 검정 |
'데이터분석 by파이썬' 카테고리의 다른 글
| t – test (0) | 2021.03.09 |
|---|---|
| 교차분석(카이제곱분석) (0) | 2021.03.07 |
| 통계분석 - 통계 개념 (0) | 2021.03.07 |
| 통계분석 - 확률과 확률분포 (0) | 2021.03.07 |
| 통계분석 (0) | 2021.03.06 |




